Februari 2002
1. Åtta torn är uppställda på ett schackbräde så att inget torn hotar något annat (en pjäs i varje rad och varje kolumn). Sju av tornen står på svarta rutor. Kan det åttonde tornet stå på en vit ruta?
2. Fido har sin hundkoja mitt i trädgården. Kojan är kvadratisk med sidan 7 dm och Fido är kopplad vid ena hörnet. Om Fido sträcker kopplet så når hans nos 24 dm från hörnet. Katten Nisse gillar att retas. Hur nära kojan kan Nisse sätta sig utan att Fido kommer åt honom?
Lösning Vinnare: -
Mars 2002
1. Med hur många nollor avslutas talet 2002! = 1*2*3*...*2002 ?
2. Till varje sida i en triangel hör en höjd - den höjd triangeln får om sidan väljs som bas. I en viss triangel är bara en av sidorna längre än sin höjd. Bestäm triangelns vinklar.
Lösning Vinnare: Ludvig Granberg, Rudbecksskolan, Sollentuna
April 2002
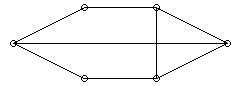
1. Flygbolaget Euroflop flyger mellan ett antal europeiska städer. Från varje stad har man direktförbindelser med högst tre andra städer. Om två städer saknar direktförbindelse kan man alltid flyga via en tredje stad. Bestäm det maximala antalet städer som Euroflop kan trafikera och rita en graf över hur flygtrafiken kan se ut. Nedan är en graf med sex städer, vilket inte är maximalt.
2. Fermats sista sats är mycket berömd och bevisades av Andrew Wiles så sent som 1994. Satsen säger att för ett heltal n > 2 finns det inte några positiva heltal x, y och z som löser ekvationen
För vilka heltal n > 0 finns det positiva heltal x, y och z som löser den "omvända" ekvationen
Lösning Vinnare: Tor Klingberg, Per Brahegymnasiet, Jönköping
Maj 2002
1. Solhöjden är solens vinkel över horisonten. Anna har en flaggstång i sin trädgård. En vacker dag mäter hon skuggan från flaggstången till 8 m vid solhöjden u. Senare samma dag är skuggan 18 m vid solhöjden v. Hon finner att u och v tillsammans är en rät vinkel. Hur lång är flaggstången? Bor Anna i Linköping?
2. Det är hög tid för matteläraren Svante att sätta betyg på eleverna Anders, Bodil, Carina, Daniel, Eija och Fredrik. Han väljer bland betygen G, VG och MVG och tänker dela ut minst ett betyg av varje slag. På hur många olika sätt kan han göra detta? Extrauppgift: Samma problem fast fler elever.
Lösning Vinnare: Andreas Myklebust, Rudbeckianska gymnasiet, Västerås
Sommaren 2002
1. Låt a, b, c och d vara positiva tal. Visa att minst en av följande tre olikheter måste vara falsk.
2. Vilken är den största möjliga arean av en fyrhörning med sidorna 1, 4, 7 och 8?
3. Andreas kastar en tärning ett antal gånger och antecknar varje kast på en papperslapp. Lisa tar lappen, suddar ut två godtyckliga tal x och y och antecknar istället talet (xy + x + y). Hon fortsätter med detta tills bara talet 1763 återstår. Andreas fick exakt en etta. Vad är summan av hans tärningskast?
Lösning Vinnare: David Berglund, Rudbeckianska gymnasiet, Västerås
September 2002
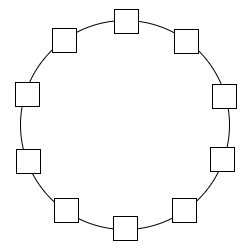
1. Går det att placera ut talen 1 till 10 i de tomma rutorna runt
cirkeln, så att summan av tre rutor i följd alltid är mindre än eller lika med
16? Ge exempel eller förklara varför det inte går!
Går det om man även
tillåter summan 17? 18?
2. Ett tredimensionellt luffarschack består av 64 kulor arrangerade som en kub (4x4x4). Hur många olika rader om fyra kulor kan man hitta i kuben?
Lösning Vinnare: Peter Welinder, Malmö Borgarskola, Malmö
Oktober 2002
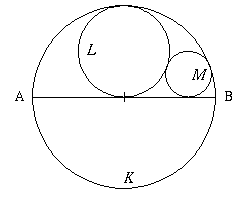
1. Låt sträckan AB vara en diameter till en cirkel K. Cirkeln L tangerar K och mittpunkten på AB. Cirkeln M tangerar K, L och AB. Bestäm kvoten mellan K:s area och M:s area!
2. Svante ska rita ett rutnät med 10 x 10 rutor. Han använder ett ritprogram där man kan rita rektanglar genom att klicka på två motstående hörn. Hur många rektanglar måste han rita för att få ett fullständigt rutnät? Testa nedan genom att klicka på punkterna! Kan du bevisa att den lösning du hittar är optimal?
Lösning Vinnare: Frida Herrgård, Rudbeckianska gymnasiet, Västerås
November 2002
1. Ett mycket litet kungarike har formen av en kvadrat med sidan 30 km. Riket har fyra små städer, en i varje hörn, men inga moderna vägar. Rita ett vägnät som binder samman de fyra städerna. Kungen har pengar till högst 82 km väg.
2. Lille Martin sitter och leker med lego-klossar. Han har klossar i fyra olika färger och med hjälp av dessa roar han sig med att bygga 24 olika torn, som alla består av fyra olikfärgade klossar. Då kommer pappa Anders in och funderar: Om man istället bygger ett högt torn, där alla de 24 småtornen kan återfinnas någonstans i det höga tornet, så borde man kunna göra det med betydligt färre klossar. Vilket är det minsta antalet lego-bitar som behövs till ett sådant torn?
Lösning Vinnare: Alexander Larsson, Rudbeckianska gymnasiet, Västerås
Julen 2002
1. Skriv talen 3,3,3,4,4,4,5,5,5,6,6,6 längs kanterna på en kub. Skriv sedan vid varje hörn summan av de tre tal som angränsar till hörnet. Kan du göra detta så att de åtta hörnsummorna blir lika?
2. Micke och Hebbe är ute och orienterar. Sent på kvällen kommer de till en landsväg söder om Linköping och beslutar att ta bussen hem till stan. Micke tror att närmaste hållplats ligger i riktning mot stan och går därför norrut med hastigheten 5 km/h. Hebbe tror motsatsen och går söderut med hastigheten 6 km/h. Båda kommer fram till sina hållplatser precis i tid för att hoppa på buss 540 från Kisa. Vem trodde rätt, om bussens hastighet var 70 km/h?
Lösning Vinnare: Maja Rullgård, Stiernhööksgymnasiet, Rättvik
Sidansvarig: jana.bjorn@liu.se
Senast uppdaterad: 2019-12-03
 Homepage
Homepage